Classes
Typedefs
REAL, 6 >
REAL, 6, 6 >
REAL, 3 >
Functions
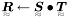 .
. 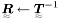 .
. 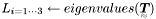 .
. 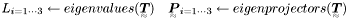 .
. 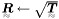 .
. 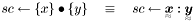
![$ \{y\}\gets\{x\}\bullet[A] \quad\equiv\quad \TeSe{y}\gets\TeSe{x}:\TeFo{A} $](form_32.png)
![$ \{y\}\gets[A]\bullet\{x\} \quad\equiv\quad \TeSe{y}\gets\TeFo{A}:\TeSe{x} $](form_33.png)
![$ [C]\gets[A]\bullet[B] \quad\equiv\quad \TeFo{C}\gets\TeFo{A}:\TeFo{B} $](form_34.png)
![$ [A]=\{x\}\otimes\{y\} \quad\equiv\quad \TeFo{A}\gets\TeSe{x}\otimes\TeSe{y} $](form_35.png)
![$ [Z] \gets a[X]+b[Y] \quad\equiv\quad \TeFo{Z}\gets a\TeFo{X}+b\TeFo{Y} $](form_73.png) .
. ![$ [A]=\alpha\{x\}\otimes\{y\}+[A] \quad\equiv\quad \TeFo{A}\gets\alpha\TeSe{x}\otimes\TeSe{y}+\TeFo{A} $](form_36.png)
![$ [D]=\alpha([A]\bullet\{x\})\otimes(\{y\}\bullet[B])+[C] \quad\equiv\quad \TeFo{D}\gets\alpha(\TeFo{A}:\TeSe{x})\otimes(\TeSe{y}:\TeFo{B})+\TeFo{C} $](form_74.png)
![$ [B]=\alpha([B]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{B} $](form_75.png)
![$ [B]=\alpha([A]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{A} $](form_76.png)
![$ s=\{x\}^T[A]\{y\} \quad\equiv\quad s=\Dc{\Dc{\TeSe{x}}{\TeFo{A}}}{\TeSe{y}} $](form_77.png)
Variables
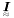 .
. 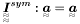 .
. 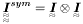 .
. 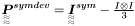 .
. 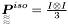 .
.
Classes | |
| class | TijTensor |
| Prof. Nakai's modified stress tensor tij. More... | |
Typedefs | |
| typedef blitz::TinyVector< REAL, 6 > | Tensor2 |
| Second Order Tensor (Mandel representation) {{{. | |
| typedef blitz::TinyMatrix< REAL, 6, 6 > | Tensor4 |
| Fourth Order Tensor (Mandel representation) {{{. | |
|
typedef blitz::TinyVector< REAL, 3 > | Tensor1 |
Functions | |
| void | Mult (Tensor2 const &S, Tensor2 const &T, Tensor2 &R) |
Tensor multiplication 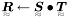 . . | |
| REAL | Norm (Tensor2 const &T) |
| Euclidian norm of a symmetric 2nd order tensor. | |
| REAL | Det (Tensor2 const &T) |
| Determinant of T. | |
| bool | Inv (Tensor2 const &T, Tensor2 &R) |
Inverse of a tensor T 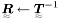 . . | |
| bool | Eigenvals (Tensor2 const &T, REAL L[3]) |
Eigenvalues (L) of a tensor T 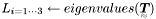 . . | |
| bool | Eigenvp (Tensor2 const &T, REAL L[3], Tensor2 P[3]) |
Eigenvalues (L) and Eigenprojectors (P) of a tensor T 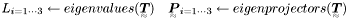 . . | |
| bool | Sqrt (Tensor2 const &T, Tensor2 &R) |
Square root of a tensor T 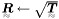 . . | |
| void | CharInvs (Tensor2 const &T, REAL I[3]) |
| Characteristic invariants of a symmetric second order tensor. | |
| void | Strain_Ev_Ed (Tensor2 const &Eps, REAL &Ev, REAL &Ed) |
| Strain Invariants. | |
| void | Stress_p_q (Tensor2 const &Sig, REAL &p, REAL &q) |
| Stress Invariants (Cambridge). | |
| REAL | Stress_q (Tensor2 const &Sig) |
| Cambridge's q deviatoric stress invariant. | |
| REAL | Sin3ThDev (Tensor2 const &S) |
| Sin3Th given deviator (S) of the stress tensor. | |
| void | Stress_p_q_S_sin3th (Tensor2 const &Sig, REAL &p, REAL &q, Tensor2 &S, REAL &sin3th) |
| Stress Invariants (Cambridge) + deviator of Sigma. | |
| bool | Stress_tn_ts (Tensor2 const &Sig, REAL &tn, REAL &ts) |
| Stress Invariants (Professor Nakai's invariants). | |
| void | Stress_P_Q (Tensor2 const &Sig, REAL &P, REAL &Q) |
| Stress Invariants (Professor Brannon's isomorphic invariants). | |
| void | Stress_P_Q_S_sin3th (Tensor2 const &Sig, REAL &P, REAL &Q, Tensor2 &S, REAL &sin3th) |
| Stress Invariants (Professor Brannon's isomorphic invariants) + deviator of Sigma. | |
| REAL | Sin3Th (REAL SI, REAL SII, REAL SIII) |
| Returns Sin3Th, given three principal values, which are not necessary sorted. | |
| void | Hid2Sig (REAL const &p, REAL const &q, REAL const &th, REAL &Sig1, REAL &Sig2, REAL &Sig3) |
| Converts hidrostatic coordinates to sigma (principal) coord (T in radians). | |
| void | Hid2Sig (REAL const *P, REAL const *Q, REAL const *T, REAL *SI, REAL *SII, REAL *SIII, int Size) |
| Converts hidrostatic coordinates to sigma (principal) coord (T in radians). | |
| void | Hid2Sig_ (REAL const &SX, REAL const &SY, REAL const &p, REAL &SI, REAL &SII, REAL &SIII) |
| Converts hidrostatic coordinates (Sx, Sy, Sz) to sigma (principal) coord (T in radians). | |
| int | JacobiRot (Tensor2 const &T, REAL V0[3], REAL V1[3], REAL V2[3], REAL L[3]) |
| Jacobi Transformation of a Symmetric Matrix (given as a Tensor2) Out: Eigenvalues (array with 3 values). | |
| int | JacobiRot (Tensor2 const &T, REAL L[3]) |
| Jacobi Transformation of a Symmetric Matrix (given as a Tensor2) Out: Eigenvalues (array with 3 values). | |
| void | Dot (Tensor2 const &A, Tensor1 const &u, Tensor1 &v) |
| REAL | Dot (Tensor2 const &x, Tensor2 const &y) |
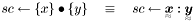 | |
| void | Dot (Tensor2 const &x, Tensor4 const &A, Tensor2 &y) |
![$ \{y\}\gets\{x\}\bullet[A] \quad\equiv\quad \TeSe{y}\gets\TeSe{x}:\TeFo{A} $](form_32.png) | |
| void | Dot (Tensor4 const &A, Tensor2 const &x, Tensor2 &y) |
![$ \{y\}\gets[A]\bullet\{x\} \quad\equiv\quad \TeSe{y}\gets\TeFo{A}:\TeSe{x} $](form_33.png) | |
| void | Dot (Tensor4 const &A, Tensor4 const &B, Tensor4 &C) |
![$ [C]\gets[A]\bullet[B] \quad\equiv\quad \TeFo{C}\gets\TeFo{A}:\TeFo{B} $](form_34.png) | |
| void | Dyad (Tensor2 const &x, Tensor2 const &y, Tensor4 &A) |
![$ [A]=\{x\}\otimes\{y\} \quad\equiv\quad \TeFo{A}\gets\TeSe{x}\otimes\TeSe{y} $](form_35.png) | |
| void | AddScaled (REAL const &a, Tensor4 const &X, REAL const &b, Tensor4 const &Y, Tensor4 &Z) |
Add scaled tensors: ![$ [Z] \gets a[X]+b[Y] \quad\equiv\quad \TeFo{Z}\gets a\TeFo{X}+b\TeFo{Y} $](form_73.png) . . | |
| void | Ger (REAL const &a, Tensor2 const &x, Tensor2 const &y, Tensor4 &A) |
![$ [A]=\alpha\{x\}\otimes\{y\}+[A] \quad\equiv\quad \TeFo{A}\gets\alpha\TeSe{x}\otimes\TeSe{y}+\TeFo{A} $](form_36.png) | |
| void | GerX (REAL const &a, Tensor4 const &A, Tensor2 const &x, Tensor2 const &y, Tensor4 const &B, Tensor4 const &C, Tensor4 &D) |
![$ [D]=\alpha([A]\bullet\{x\})\otimes(\{y\}\bullet[B])+[C] \quad\equiv\quad \TeFo{D}\gets\alpha(\TeFo{A}:\TeSe{x})\otimes(\TeSe{y}:\TeFo{B})+\TeFo{C} $](form_74.png) | |
| void | Scale (REAL const &a, Tensor4 &B) |
![$ [B]=\alpha([B]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{B} $](form_75.png) | |
| void | CopyScale (REAL const &a, Tensor4 const &A, Tensor4 &B) |
![$ [B]=\alpha([A]) \quad\equiv\quad \TeFo{B}\gets\alpha\TeFo{A} $](form_76.png) | |
| REAL | Reduce (Tensor2 const &x, Tensor4 const &A, Tensor2 const &y) |
![$ s=\{x\}^T[A]\{y\} \quad\equiv\quad s=\Dc{\Dc{\TeSe{x}}{\TeFo{A}}}{\TeSe{y}} $](form_77.png) | |
| int | __initialize_the_I (Tensor2 &theI) |
| int | __initialize_the_IIsym (Tensor4 &theIIsym) |
| int | __initialize_the_IdyI (Tensor4 &theIdyI) |
| int | __initialize_the_Psd (Tensor4 &thePsd) |
| int | __initialize_the_Piso (Tensor4 &thePiso) |
Variables | |
| Tensor2 | I |
Second order identity (symmetric/Mandel's basis) 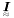 . . | |
| Tensor4 | IIsym |
Forth order identity (symmetric/Mandel's basis) 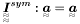 . . | |
| Tensor4 | IdyI |
Forth order tensor given by I dyadic I, in which I is the second order identity (symmetric/Mandel's basis) 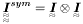 . . | |
| Tensor4 | Psd |
Forth order "symmetric-deviatoric" tensor 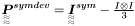 . . | |
| Tensor4 | Piso |
Forth order "isotropic" tensor 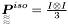 . . | |
| int | __dummy1 = __initialize_the_I(I) |
| int | __dummy2 = __initialize_the_IIsym(IIsym) |
| int | __dummy3 = __initialize_the_IdyI(IdyI) |
| int | __dummy4 = __initialize_the_Psd(Psd) |
| int | __dummy5 = __initialize_the_Piso(Piso) |
 1.4.7
1.4.7